Analyzing the Semantic Web
The data set that describes the Semantic Web is a classic example of Big Data. The set I used for my analysis is known as the Billion Triples dataset. It contains a billion entries in a format known as RDF triples. This format requires statements to be expressed in the form:
Subject Predicate Object For example, to say something like "Bob is Tim's father" in RDF you would write
Subject:[Bob] Predicate:[is the father of] Object:[Tim]In the Semantic Web, the entities in the RDF triples are not confined to only people, but can be anything described by a URI (Universal Resource Identifier)--literally anything. The Billion Triples database therefore contains a ton of information describing the relationships of interconnected people/places/things/companies. We can treat this set as a directed graph where each entry represents an edge between two vertices (the subject and object).
 |
| An example of a directed graph. If this were to represent the Semantic Web, each of the circles would be represented by a URI. The arrows are drawn whenever a subject points to an object in RDF. |
Analyzing graphs like this is a standard task for data scientists, and one common quantity to compute is the out-degree of each node. This represents the number of objects that a given subject links to. In the example graph above there are 2 arrows leaving node 7. Therefore node 7 has an out-degree of 2. We can learn a lot about a graph by computing a histogram of the out-degree of all its nodes.
However, the Billion Triples data set is so large (>0.5 TB) that a single computer can't handle it. Instead we have to use a cluster of computers, each operating on a small chunk of the data. This situation refers to a classic computer programming model known as MapReduce in which common tasks get mapped to a single machine which then performs some simple aggregate function (like counting) in the reduce step.
When files are this large, they can't be stored in traditional file systems. Instead, distributed file systems like Hadoop break up large files into many smaller chunks stored on separate machines across a network. In this way, file access can be parallelized and you can scale up your MapReduce jobs into the cloud. This is exactly what I did for my analysis of the Semantic Web.
Using Amazon Web Services, I pulled the data set from S3 storage and analyzed it on their cloud computing servers. To setup the MapReduce jobs, I used the programming tool Pig. This tool coordinates the resources of the 20 compute nodes I ran my script on. In my Pig script I group the entries by subject, then count the number of entries for each subject (the out-degree). Then I count the number of subjects having out-degree d for my histogram. After 4 hours of running in the cloud, I get the following plot:
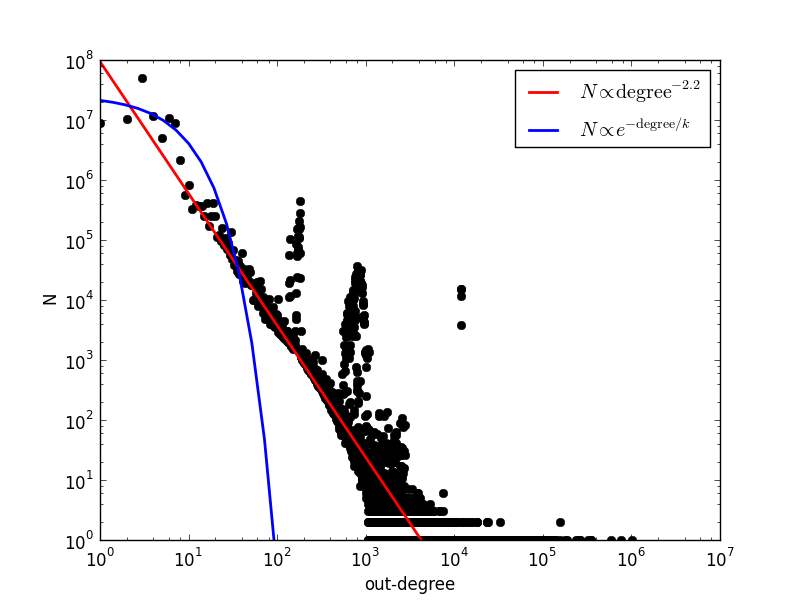 |
| The distribution of subjects having various values for their out-degree. Fits to the data were obtained with the optimize.curve_fit package in SciPy. |
The code I wrote to generate this plot fits an exponential function (blue) and a powerlaw function (red) to the distribution. A result from graph theory is that the out-degree histogram of a random graph will follow an exponential distribution. Since the blue line is a terrible fit to the data, we can tell that the Semantic Web is not a random graph. Instead, we can see that a powerlaw with index -2.2 does a pretty good job at fitting most of the data.
This index of -2.2 in a powerlaw distribution is a number that frequently comes up in the analysis of networks. Researchers studying the patterns of phone calls among AT&T's customers also find the exact same distribution with the exact same index. There is something fundamental in the way networks organize themselves such that they produce powerlaw histograms with an index near -2.2. I find it really interesting that a network of telephone calls among friends displays the same properties as a catalog of the relationships between everything in the Semantic Web. Even more interesting was the cloud computing I got to do (for free with a student grant from AWS, I should add!).
Leave a Comment